This week in String Theory: overcoming writer's block; designing characters
- Anthony

- Dec 24, 2023
- 9 min read
Hello everyone! It's Christmas Eve as I'm writing this, at a very muggy 21°C with light showers.
This post is rather information-dense, so I'll warm you up with some concept art I've been working on. Some of these designs are the first real visualizations of the characters and are thus not final. Grace was my first attempt at this format, which is why she looks a little different (unfinished).
I've also put them roughly together in a lineup to display their height differences. Of all the designs, Keats' is the one I'm most happy with. I think they've all turned out accurate to my vision, but Keats is exact to the mental image I've had of him, which is really quite rare for me as an artist.
Charlie also turned out great; I'm really pleased with his depiction. I really like Harvey's side-profile which shows a more humanized side of him beyond his grumpy/long-suffering probation officer depiction. Ulysses' side profile, though not anatomically ideal, displays his sense of guilt and humility quite well.
As these were intended more to be quick sketches than polished pieces, I'm more than happy to share them here.
I'll talk about designing Glensyde's coat of arms and school uniform in another blog post, because that was its whole own adventure!
On dealing with writer's block:
I mentioned in my last post that String Theory utilizes each issue as a building block in developing the reader's understanding of the phenomena behind the plot. As each issue relies on the issues prior to it to successfully divulge lessons to the reader in a comprehensible manner, it's common for me to get stuck trying to smoothly incorporate the 'lessons' into the story.
Issue three, "Hollow Earth," focuses on probability and logic.
Writing about logic went quite smoothly, primarily because Susanne K. Langer's Symbolic Logic was fresh in my mind. It's a truly brilliant introduction to its namesake, as it requires absolutely no knowledge of mathematics to begin reading. The information can become quite dense at some points, which requires you to really slow down and wade through it at your own rate of comprehension, but I don't think this is a weakness of the work; it's written in such a way where skim-reading it wouldn't do you much good at all.
The knowledge within Symbolic Logic is paramount not only to the fields of mathematics and science, but also philosophy, debate, language, even day-to-day life. I will certainly do a proper write-up on what this book has meant to me, and I very much look forward to that, but for the time being I will run through what aspects have influenced String Theory in particular.
Langer's work does a great job of breaking down the different forms relationships can take, and how we can symbolize these relationships. Consider how the term "is" has been used in the following propositions, which I've taken directly from Symbolic Logic:
The rose is red. (Ascribes a property to a term.)
Rome is greater than Athens. (Asserts the relation, "greater than.")
Barbarossa is Frederick I. (Expresses identity.)
Barbarossa is a legendary hero. (Indicates membership in a class.)
To sleep is to dream. (Sleeping entails dreaming.)
God is. (Existence.)
Now, if we were to replace each "is" with the appropriate symbols within the field of logic, the term "is" reveals itself as that which can take on a variety of meanings, depending on the relationship it refers to:
R(rose) (if R represents the property "is red"); or, Rose ∈ red (objects).
Rome > Athens.
Barbarossa = Frederick I.
Barbarossa ∈ legendary hero.
To sleep ⊢ to dream.
∃! God.
This exemplifies the limitations of natural language when it comes to representing logical relationships, and the significant utility that comes with assigning symbols to each relationship.
If you want to build up an elaborate conceptual structure, we must have recognizable concepts, not subjective and incommunicable mental pictures. It does not make any difference what sort of mental picture embodies a concept; all that counts in science is the concept itself.
— Chapter 3.2 (65).
The third issue of String Theory opens with the tasteful combination of a police chase and a violent debate on whether or not the zombie-like people cropping up around Glasgow are, in fact, zombies. Now, from a contextual standpoint, they certainly seem to be zombies. It's argued that because these people are in a state of being both dead and alive, they are zombies.
However, these people never actually died in the first place. A zombie, according to my definition, is a dead human whose body is reanimated due to an infection with the aim of spreading the infection to other humans. The zombie-like people in String Theory exist in a paradoxical state of being half-alive and half-dead — which is not what a zombie actually is.
Zombies could be considered a subset or sub-class of cannibals. You would say all zombies are cannibals, but you wouldn’t say all cannibals are zombies. The first statement is indisputably true, the second is borderline nonsense.
This relationship is represented in symbolic logic as follows:
(x): (x ∈ Z) ⊢ (x ∈ C) and ∃x: (x ∈ C) ∧ (x ∉ Z)
Where C represents the set 'Cannibals' and Z represents the set 'Zombies'.
Written in plain English, this means that if an individual "x" is a zombie, they are therefore a cannibal. However, if x is a cannibal, they aren't necessarily also a zombie, but they could be. (The symbol ∃ means "at least one exists." So, there's one or more individuals "x" that are cannibals but are not zombies. For example, Hannibal Lecter falls within ∃x.)
A subset of a class must be composed of members who would all fit into the class above it. Zombies have the following elements — these would have to all be true in order for someone to be considered a member of the class.
Zombies must be infected with something,
which causes them to die or become braindead,
then their corpse must become reanimated,
in order to eat people,
thus spreading the infection to the people they eat.
The not-zombies of String Theory (which I will refer to as 'Schrödingers') are:
Infected with something,
which causes them to become vegetative, not die, nor become braindead,
making it false that their corpse is reanimated, as they were never corpses,
and they also do not eat people,
and it is unclear how the infection spreads,
and whether or not it’s contagious.
Therefore, Schrödingers only concretely share one element with zombies, being that they are infected with something, and thus cannot be logically classified as zombies, nor as a subclass of zombies.
Anyway, on to probability.
After all that logic stuff went onto the page pretty smoothly, I was confident I could get through the second part of the issue without an issue. However, when it came to writing about probability, I really hit a wall.
Writing about these topics (where I'm very much a layman) is like spinning a hundred plates. It's very difficult to regulate how my working memory stores technical information that needs to remain connected to other technical information. I omit or lose knowledge of things I've researched for String Theory at highly inconvenient times. If your mind doesn't efficiently store and retrieve what you actually know, it can feel identical to knowing nothing at all.
Probability is highly correlated with everything around us, which is why I chose it as one of the first building blocks of the story's lessons. When you understand what is meant by probability, it makes it so much easier to comprehend the movement of electrons, the behaviour of time, new theories regarding gravity, atomic half-lives, concepts such as 'quantum foam' and 'spin networks', Hawking radiation, Schrodinger's cat, the heat death of the universe, and a variety of other fun stuff. The potential of probability is often demonstrated in thought experiments, often those which reflect very extreme cases to prove a point. If you've ever heard of monkeys on a typewriter, you likely have some insight into the correlation between time, infinity, and probability.
No, between now and the heat death of the universe, a Boltzmann brain is not going to appear, because that will take at least 10↑↑(10^50) years. The universe will end in 1.7×10^106 years, which is a period of time so much substantially shorter that there's really no way of grasping it.
But the odds aren't zero, either. As long as the probability of something is not zero, it will happen within a span of time between now and infinity. That's kind of the point of quantifying probability in the first place, even with such insanely large numbers. It's fun!
In "Hollow Earth", I decided to use Schrodinger's cat, and its spinoff episode that is quantum immortality, to represent the philosophy behind probability.
Note: Talking about quantum immortality can make certain people very upset, including theoretical physicists, because they feel it is, at times, taken too literally. There have been some very sad and tragic cases wherein the thought experiment has led people towards drastic actions; people with mental health disorders are particularly vulnerable. Please exercise caution in researching this subject if discussions of suicide and/or existential topics are distressing for you.
It turns out that the use of quantum immortality slots in perfectly with the story, as it builds directly on what was established within the logic lesson. I was able to create a dialogue surrounding paradoxes within the probabilistic behaviour of quantum particles, which thus also clarified what is meant by the Schrödingers being both alive and dead.
An element of the story involves the fluctuation of "probability fields" based on an interdimensional disease. That which is impacted by this fluctuation may experience extreme variations from the standard deviation of probability, for example, due to the warping of how time "flows." Time is, of course, a topic to be addressed in a later issue. For the sake of brevity I will drop the bombshell that time very well may not be linear and it is only the human mind which organizes it as linear. In my own opinion the experience of time is subjective to the extent I would classify it as qualia.
Put it this way: consider time not as some kind of flat, linear, consistent blanket that lies upon all things in equilibrium, but instead as something chaotic, fuzzy, porous, whizzing around and fluctuating and perhaps even taking shape, not being "linear", as in from point A to point B to point C, but instead functioning much as our own memories do, where we jump from one experience in time to another with little concern for chronology, with lots of variations in the details of the memories each time they are called upon, able to shuffle and organize and replace memories as though they are a pile of photographs on the floor. It makes it far easier to organize the photos into a chronological album, but that's not really necessary for understanding the context within each snapshot. Unless, of course, your evolving brain happens to find advantage in organizing time in a linear fashion.
This way of thinking about time is somewhat of a basis for quantum immortality. Imagining time as something less structured and set, and instead as probabilistic and 'fuzzy', infinitely layered upon itself and able to branch much as a fractal in any way it chooses, entertains the thought that due to the uncertainty principle, there exists an infinite amount of alternate timelines wherein all possible arrangements of particles at any given point are able to manifest.
This is why there is a universe where you are the President of the United States. It's why there's a universe where you are the President of the United States, but everything is a little to the left.
It's also why there's a universe where you are immortal. If we perceive time as qualia, that which is subjective to an individual's experience, we can also broaden it to the conjecture that consciousness is a form of qualia. See philosophical zombies. (These are not defined as zombies within my logical set but whatever.)
I have argued before that death is impossible to experience because it falls outside of the realm of consciousness. You can experience dying, but you can never 'be' dead, because death means that you can no longer 'be'. In this sense the probability of you ever actually being dead from your own perspective is zero.
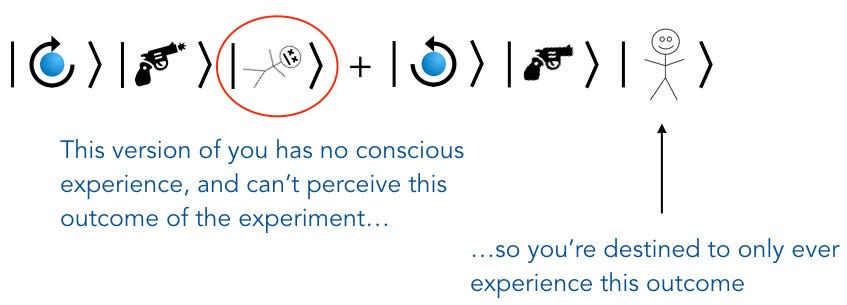
Essentially, if all particles are superimposed, and all moments in time are superimposed, every iteration of time creates a new branch, one where you're dead, another where you're alive, stretching forever into infinity.
(So what about the Schrödingers in String Theory? Doesn't that moot the entire disease if everyone is perpetually in the state of being both dead and alive? Well, the difference is that the disease allows you to see and/or experience the superposition. I won't go in depth, but essentially: they are seeing and/or experiencing more than one timeline.)
There is theoretically a universe where I had a stroke writing this sentence and dropped dead before I could finish it. Whoever finds me will be very spooked to read this sentence. I might have the stroke now, instead. Or now. How about now? Maybe someone with a gun has walked up to my window and shot me in the head. Maybe all the particles to form a gun randomly came together and manifested a gun in my room, much like a Boltzmann brain, to shoot me in the head. These all have happened, these all have not happened, these all will happen, and these all will not happen.
If that doesn't summarize what probability is all about, I don't know what will.
Until next time!
Before you go, there is a new Zack the Mischief-Making Cat strip! It's a bit avant-garde but I was laughing the whole time I was drawing it. In my childhood version of the comic there was a kangaroo called Jack. I think drawing him as realistically (and 'Jacked') as I can is very funny and I will probably keep it as a staple of his character. (Also, not ever addressing that he looks far older than Zack does, yet Zack is the only one treated as though he's too old to be in third grade.)
Thank you for checking in with the blog this week! It's been quite the grind over the past few days, but I'm very satisfied with the progress. I will aim to update you on String Theory weekly, depending on how balanced that feels.





















Comentarios